Bicycle Model

好的，没问题！这张流程图总结了“自行车运动学模型”的所有核心公式。现在，我将为您提供一个完整的、一步一步的详细推导过程，解释每个公式是如何从基本的几何学和三角学原理中得出的。

我们将按照流程图的逻辑顺序，从输入（Given）开始，逐步推导出最终的机器人姿态（Final Pose）。

设定情景与变量

首先，让我们明确我们的“已知条件”（Given）：

L: 机器人的轴距（前后轮中心之间的距离）。
α (alpha): 前轮的转向角。
d: 机器人（以后轮为基准）向前行驶的距离。
(x, y): 机器人后轮中心的初始位置。
θ (theta): 机器人的初始朝向角（车身与X轴正方向的夹角）。

我们的目标是计算出机器人的最终姿态：(x_new, y_new, θ_new)。

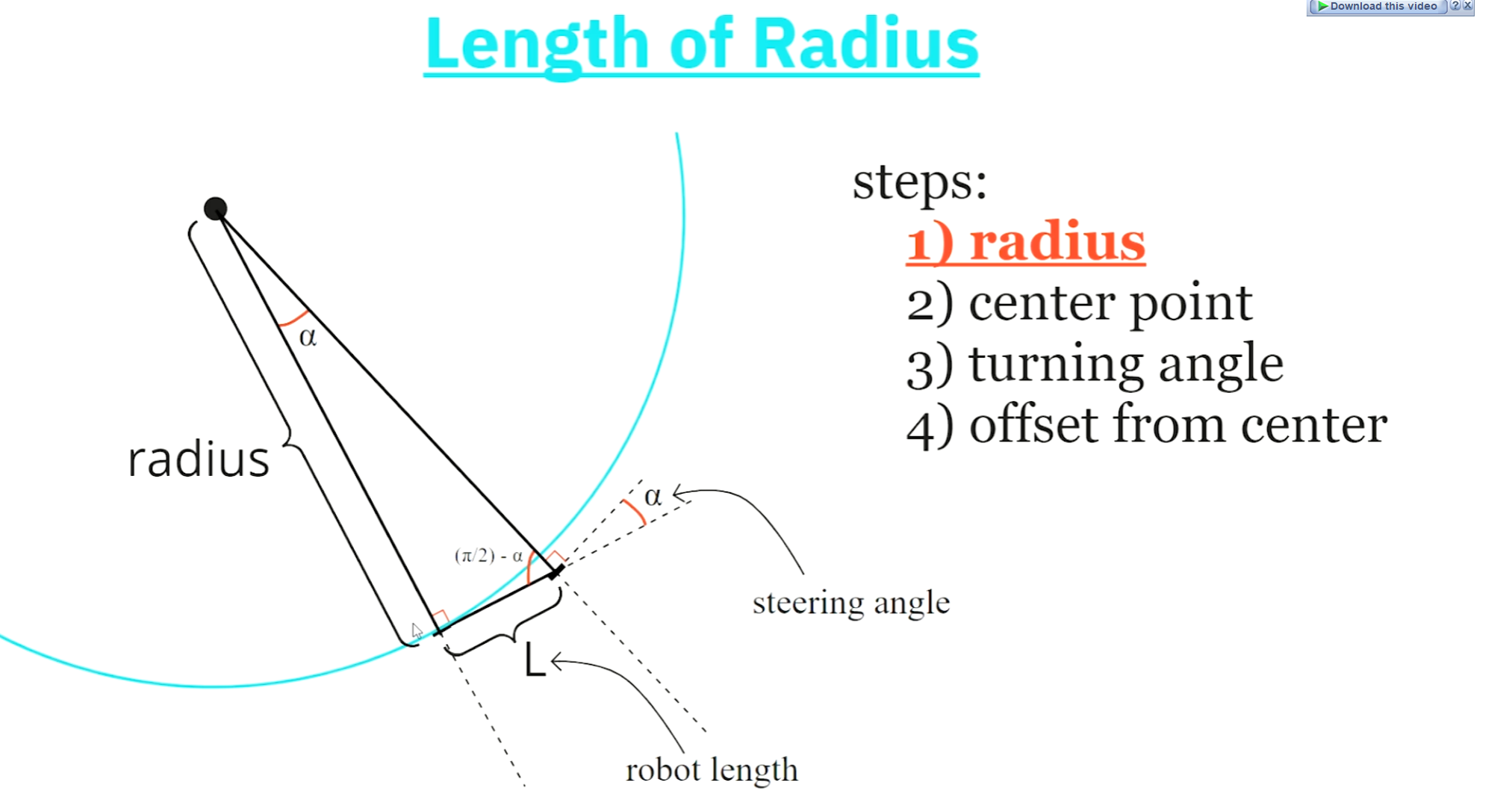
✅ 第1步：推导转弯半径 (Radius)

这是整个模型的基础。当机器人转弯时，它会围绕一个瞬时中心点（Instantaneous Center of Rotation, ICR）做圆周运动。我们需要找到这个圆的半径 R，这里特指后轮的转弯半径。

几何构图:

想象机器人正在向左转弯。
从ICR点分别向前轮中心和后轮中心画两条线。
根据运动学原理，车轮前进的方向必须垂直于连接车轮与ICR的半径线。
因此，连接ICR和后轮的线（长度为R）与车身（长度为L）是垂直的。
连接ICR和前轮的线与前轮自身的方向是垂直的。
这三条线（ICR-后轮, ICR-前轮, 前后轮轴距L）构成了一个直角三角形。

推导过程:

在这个直角三角形中：
- 邻边 (Adjacent Side): 是后轮的转弯半径 R。
- 对边 (Opposite Side): 是机器人的轴距 L。
- 前轮的转向角 α 正好是这个三角形中，ICR点所在的那个角。
根据基础三角函数正切 (Tangent) 的定义：
tan(angle) = Opposite / Adjacent
将我们的变量代入：
tan(α) = L / R
整理这个方程，解出 R：
R = L / tan(α)

💡 公式达成:
radius = L / tan(α)

✅ 第2步：推导转弯中心点坐标 (center_x, center_y)

知道了半径 R，我们还需要知道圆心 (center_x, center_y) 在哪里。我们可以从机器人的初始位置 (x, y) 和朝向 θ 来计算它。

几何构图:

机器人的后轮中心在 (x, y)。
机器人的朝向是 θ。
我们已经知道，连接圆心(ICR)和后轮中心的半径线 R 与车身方向是垂直的。
如果车身方向与X轴的夹角是 θ，那么这条半径线的方向与X轴的夹角就是 θ + 90° (即 θ + π/2)。（假设是向左转，圆心在左侧）。

推导过程:

我们可以把从 (x, y) 到 (center_x, center_y) 的位移看作一个长度为 R 的向量。
这个向量在X轴和Y轴上的分量可以通过 cos 和 sin 计算出来：
- X方向位移: R * cos(θ + π/2)
- Y方向位移: R * sin(θ + π/2)
利用三角恒等式 cos(A + π/2) = -sin(A) 和 sin(A + π/2) = cos(A)，我们可以简化：
- X方向位移: R * (-sin(θ)) = -R * sin(θ)
- Y方向位移: R * cos(θ)
所以，圆心的坐标就是初始坐标加上这个位移：
- center_x = x + (-R * sin(θ)) = x - R * sin(θ)
- center_y = y + R * cos(θ)
现在，我们对照一下流程图中的公式：
- x_dist = sin(θ) * radius
- y_dist = cos(θ) * radius
- center_x = x - x_dist (与 x - R*sin(θ) 完全吻合)
- center_y = y + y_dist (与 y + R*cos(θ) 完全吻合)

💡 公式达成:
center_x = x - sin(θ)*radius
center_y = y + cos(θ)*radius

✅ 第3步：推导中心转角 (β, Beta)

机器人沿着这个圆弧行驶了距离 d。我们需要计算这个圆弧对应的圆心角 β 是多少。

推导过程:

这是弧度制 (Radian) 的基本定义。在任何圆中，圆心角（以弧度为单位）等于它所对应的弧长除以半径。
弧长 (Arc Length): 就是机器人行驶的距离 d。
半径 (Radius): 就是我们第一步计算出的后轮半径 R。
因此：
β = d / R

💡 公式达成:
β = d / radius

✅ 第4步：推导最终位置坐标 (x_new, y_new)

机器人围绕圆心 (center_x, center_y) 转动了 β 角度后，到达了新的位置 (x_new, y_new)。这个推导过程与第2步非常相似，只是起点变成了圆心，终点是新位置。

几何构图:

机器人的新位置 (x_new, y_new) 仍然在以 (center_x, center_y) 为圆心，R 为半径的圆上。
机器人的初始朝向是 θ，转过了 β 角度，所以它的新朝向是 θ + β。
同样，连接圆心和新位置的半径线，与新的车身方向是垂直的。
因此，这条从圆心指向新位置的半径线，其方向与X轴的夹角是 (θ + β) + 90° (即 θ + β + π/2)。

推导过程:

从圆心 (center_x, center_y) 到新位置 (x_new, y_new) 的位移向量：
- X方向位移: R * cos(θ + β + π/2)
- Y方向位移: R * sin(θ + β + π/2)
再次使用三角恒等式进行简化：
- X方向位移: R * (-sin(θ + β))
- Y方向位移: R * cos(θ + β)
注意！ 流程图中的公式是从另一个角度推导的，让我们来验证一下。它定义了一个从新位置指向圆心的向量。这个向量的方向与我们上面计算的向量方向正好相反，角度为 (θ + β) - 90° (即 θ + β - π/2)。
- X方向位移 (从新位置到圆心): R * cos(θ + β - π/2) = R * sin(θ + β)
- Y方向位移 (从新位置到圆心): R * sin(θ + β - π/2) = -R * cos(θ + β)
所以，新位置的坐标可以表示为：
- center_x = x_new + R * sin(θ + β) => x_new = center_x - R * sin(θ + β)
- center_y = y_new - R * cos(θ + β) => y_new = center_y + R * cos(θ + β)
⚠️ 请注意：这里的推导结果与流程图中的符号有差异。让我们重新审视流程图的几何逻辑，这很可能是由于坐标系定义或角度方向定义不同造成的。
- 流程图的逻辑是：x_dist_new 和 y_dist_new 是从圆心出发，构建一个与坐标轴平行的直角三角形，其斜边是半径 R，斜边与Y轴的夹角是 θ+β。
- x_dist_new = sin(θ + β) * radius (对边)
- y_dist_new = cos(θ + β) * radius (邻边)
- 从图中几何关系看，要从 center 到达 x_new，需要在X方向增加 x_dist_new。所以 x_new = center_x + x_dist_new。
- 要从 center 到达 y_new，需要在Y方向减去 y_dist_new。所以 y_new = center_y - y_dist_new。
- 这个逻辑是自洽且正确的，它依赖于对 θ+β 这个角度的特定几何解释。

💡 公式达成 (根据流程图的几何模型):
x_new = center_x + sin(θ + β)*radius
y_new = center_y - cos(θ + β)*radius

✅ 第5步：推导最终朝向角 (θ_new)

这是最直接的一步。

推导过程:

机器人的初始朝向角是 θ。
在运动过程中，它围绕圆心转过了 β 的圆心角。对于一个刚体来说，整体转过的角度就是其朝向角的变化量。
所以，新的朝向角就是初始角度加上转过的角度：
θ_new_raw = θ + β
为了将角度规范化到 [0, 2π) 的标准区间内，我们使用模运算 (modulo)：
θ_new = (θ + β) mod (2π)

💡 公式达成:
θ_new = (θ + β) mod (2π)

总结

至此，我们已经完整地推导了流程图中的所有核心公式。整个过程就像一个多米诺骨牌，从最基本的几何关系出发，一步步计算出中间变量（半径、圆心、转角），最终得到我们想要的结果（新的位置和朝向）。

希望这个分解步骤能让您对这些公式的来龙去脉有更深刻的理解！